Voici un article que j'ai écrit en tant qu'invitée sur le blog de Béatrice Lhuillier, spécialiste de la pensée visuelle (https://www.imaginographe.com/) :
Cartonner en maths au collège grâce à la pensée visuelle !
Cartonner en maths au collège grâce à la pensée visuelle !
Car je suis persuadée qu'en maths aussi - et pas seulement en géométrie - travailler avec crayon et papier en main est très important : illustrer, gribouiller, représenter, schématiser... tout est permis !
La première partie est détaillée ci-dessous :
La première partie est détaillée ci-dessous :
Et si le dessin vous sauvait en maths ?
Faire des maths un jeu… Bof ! Mais peut-être pouvez-vous mettre du jeu et du fun dans la forme ?
Et si vous troquiez le cahier 96 pages petits carreaux contre des feuilles blanches et des feutres ? Plus sympa, non ?
Faire des maths un jeu… Bof ! Mais peut-être pouvez-vous mettre du jeu et du fun dans la forme ?
Et si vous troquiez le cahier 96 pages petits carreaux contre des feuilles blanches et des feutres ? Plus sympa, non ?
Fun + Visuel = Motivation + efficacité
Voilà une belle équation !
Comment la pensée visuelle aide à actionner les différents processus mentaux d’apprentissage ?
En quoi mettre plus de « visuel » dans sa façon d’apprendre permet de gagner en efficacité ?
La pensée visuelle agit sur les différents processus mentaux d'apprentissage
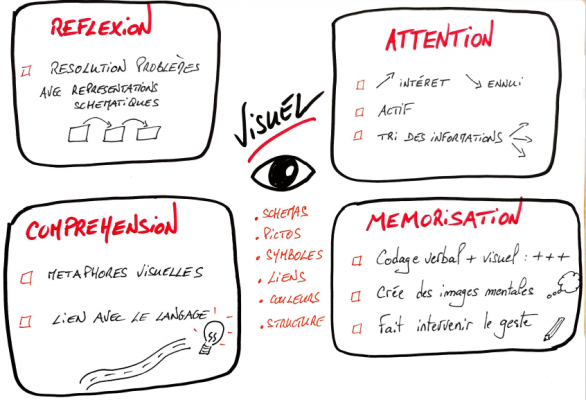
L'attention
C’est la porte d’entrée de l’activité mentale.
Par l’attention, nous entrons en relation avec l’objet ou le sujet d’étude. Ceci suppose de faire un tri dans toutes les informations et les sollicitations qui nous parviennent.
Le fait de prendre un crayon en main, de se focaliser sur sa feuille, sur les liens entre les idées, sur les couleurs et sur la façon d’illustrer tel ou tel point permet de diriger et de maintenir son attention sur le sujet.
Une page colorée, proposant des dessins et une structuration spatiale, apparait comme bien moins ennuyeuse à créer ou à lire qu’un texte noir et blanc.
Par ailleurs, le fait de synthétiser les informations en mots-clés et de les hiérarchiser permet d’éviter l’éparpillement des pensées.
Par l’attention, nous entrons en relation avec l’objet ou le sujet d’étude. Ceci suppose de faire un tri dans toutes les informations et les sollicitations qui nous parviennent.
Le fait de prendre un crayon en main, de se focaliser sur sa feuille, sur les liens entre les idées, sur les couleurs et sur la façon d’illustrer tel ou tel point permet de diriger et de maintenir son attention sur le sujet.
Une page colorée, proposant des dessins et une structuration spatiale, apparait comme bien moins ennuyeuse à créer ou à lire qu’un texte noir et blanc.
Par ailleurs, le fait de synthétiser les informations en mots-clés et de les hiérarchiser permet d’éviter l’éparpillement des pensées.
La mémorisation
Notre cerveau traite une image bien plus rapidement qu’un mot. Remplacer ou rajouter une illustration à une information va donc renforcer la mémorisation de celle-ci.
Comment par exemple bien ancrer en mémoire les théorèmes phares du collège : Pythagore et Thalès ? Et surtout les liens entre :
Comment par exemple bien ancrer en mémoire les théorèmes phares du collège : Pythagore et Thalès ? Et surtout les liens entre :
- le théorème de Pythagore et les triangles rectangles
- le théorème de Thalès et les droites parallèles et les droites sécantes

Nous plaçons souvent chronologiquement la compréhension avant la mémorisation.
Nous mémoriserons mieux quelque chose que nous avons bien compris. Mais il est également important de travailler la mémorisation en tant que telle : « apprendre par cœur » reste fondamental.
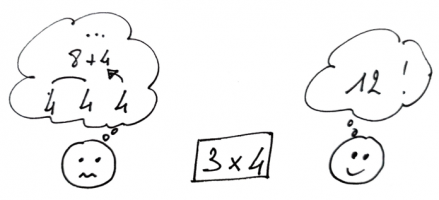
Les tables de multiplication en sont un parfait et fameux exemple.
C’est important de comprendre que 3 x 4 c’est 4 + 4 + 4 et on peut donc retrouver le résultat ainsi. Mais il sera beaucoup plus rapide et efficace de connaitre par cœur le résultat (3x4=12) : on gagne du temps, on économise de l’énergie, la tâche est automatisée et donc le cerveau est plus disponible pour la réflexion par exemple !
Nous mémoriserons mieux quelque chose que nous avons bien compris. Mais il est également important de travailler la mémorisation en tant que telle : « apprendre par cœur » reste fondamental.
Les tables de multiplication en sont un parfait et fameux exemple.
C’est important de comprendre que 3 x 4 c’est 4 + 4 + 4 et on peut donc retrouver le résultat ainsi. Mais il sera beaucoup plus rapide et efficace de connaitre par cœur le résultat (3x4=12) : on gagne du temps, on économise de l’énergie, la tâche est automatisée et donc le cerveau est plus disponible pour la réflexion par exemple !
La réflexion
Réfléchir sur un sujet permet justement de mobiliser ses connaissances c’est-à-dire les informations que l’on a mémorisées. L’important va être de les trier et de les relier aux données du problème.
A tous les niveaux scolaires, la stratégie permettant de partir du concret pour aller vers l’abstrait est particulièrement efficace pour enseigner les mathématiques. Elle se décompose en trois stades :
A tous les niveaux scolaires, la stratégie permettant de partir du concret pour aller vers l’abstrait est particulièrement efficace pour enseigner les mathématiques. Elle se décompose en trois stades :
- Le concret : on utilise des objets (des cubes, des Legos…) pour représenter les données mathématiques. C’est le stade de la manipulation sensorielle.
- La représentation visuelle : dessins, schémas…
- L’abstrait : on utilise des symboles et des nombres mathématiques.
La représentation visuelle est une compétence importante : la visualisation et les capacités de raisonnement spatial sont nécessaires pour résoudre des problèmes en maths et en sciences. Mais cette compétence n’est pas forcément naturelle, elle doit être acquise et pratiquée.
On peut distinguer deux types de représentation :
- Figurative : elle représente l’aspect visuel des objets, c’est un dessin.
- Schématique : elle représente les relations entre les objets.
On peut distinguer deux types de représentation :
- Figurative : elle représente l’aspect visuel des objets, c’est un dessin.
- Schématique : elle représente les relations entre les objets.
La représentation schématique est plus efficace pour résoudre des problèmes mathématiques.
Prenons l’exemple de ce problème : (extrait de l’article « L’utilisation efficace des diagrammes en mathématiques » de Jeffrey MacCormack et Ian Matheson, https://www.taalecole.ca/lutilisation-efficace-des-diagrammes/).
Ahmed participe à un triathlon de 78 kilomètres. Il doit parcourir une distance de 3 kilomètres à la nage.
La distance qu’il doit parcourir à vélo est quatre fois plus grande que celle qu’il doit parcourir à la course.
Quelle distance parcourra-t-il en vélo durant le triathlon?
Voici un exemple de représentation figurative :
Ahmed participe à un triathlon de 78 kilomètres. Il doit parcourir une distance de 3 kilomètres à la nage.
La distance qu’il doit parcourir à vélo est quatre fois plus grande que celle qu’il doit parcourir à la course.
Quelle distance parcourra-t-il en vélo durant le triathlon?
Voici un exemple de représentation figurative :
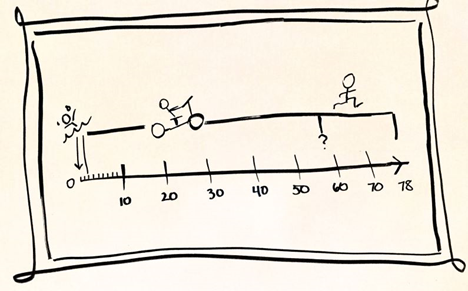
Sont représentées la ligne de distance et les 3 étapes du triathlon : nage, vélo, course. On peut en déduire que la distance vélo+course est de 75 km mais ce schéma ne permet pas de déterminer la distance parcourue à vélo.
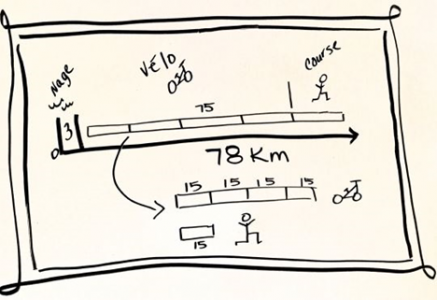
Et voici une représentation schématique faisant apparaitre des blocs pour montrer que la distance à vélo est 4 fois plus grande que celle parcourue à la course. Ce qui fait 5 blocs égaux qui représentent en tout 75 km (5x15).
L’athlète parcourt donc 60 kms à vélo.
Ce schéma permet de représenter le problème et de le résoudre.
L’athlète parcourt donc 60 kms à vélo.
Ce schéma permet de représenter le problème et de le résoudre.
Les représentations visuelles, notamment les schémas comme nous venons de le voir, permettent donc aux élèves de réfléchir et de résoudre des problèmes d’une façon différente. Cette possibilité ouvre les horizons et peut fortement soulager et soutenir certains jeunes mal à l’aise dans cet univers trop abstrait ! Il est possible de trouver son propre cheminement et d’organiser l’information à sa manière, tout en étant guidé pour trouver des représentations pertinentes.
Il est plus efficace de se concentrer sur la représentation des liens entre les éléments que sur les éléments eux-mêmes.
La compréhension
Bien souvent en maths, on entend ce genre de phrases ou de sentences : « il ne comprend rien » ou « elle n’a rien compris à l’exercice ». Mais ces difficultés de compréhension peuvent en fait se révéler être des problèmes d’attention ou être dues à des réponses trop spontanées sans faire appel à la réflexion, comme dans ce genre de problème :


Le sens des mots est en effet particulièrement important en mathématiques. Cette dimension linguistique constitue souvent un obstacle à la compréhension d’un concept.
Une représentation visuelle va permettre de combiner une représentation du sens du mot (sa signification) et de son sens mathématique (le concept).
Une représentation visuelle va permettre de combiner une représentation du sens du mot (sa signification) et de son sens mathématique (le concept).
Exemples de représentations combinant sens du mot et sens mathématique

Termes statistiques :
Etendue : écart entre la valeur la plus grande et la valeur la plus petite
Etendue : écart entre la valeur la plus grande et la valeur la plus petite

Le théorème de Pythagore :
Certains élèves retiennent de Pythagore l’idée vague d’une égalité entre les longueurs mais les « carrés » ont disparu.
Cela donne par exemple : BC = AB +AC.
Une méthode visuo-spatiale permet de « voir » que l’aire du carré construit sur l’hypoténuse est égal à la somme des 2 autres aires (la manipulation par des Lego comme ci-dessous permet vraiment de l’expérimenter en empilant les cubes verts sur les cubes rouges).
Certains élèves retiennent de Pythagore l’idée vague d’une égalité entre les longueurs mais les « carrés » ont disparu.
Cela donne par exemple : BC = AB +AC.
Une méthode visuo-spatiale permet de « voir » que l’aire du carré construit sur l’hypoténuse est égal à la somme des 2 autres aires (la manipulation par des Lego comme ci-dessous permet vraiment de l’expérimenter en empilant les cubes verts sur les cubes rouges).

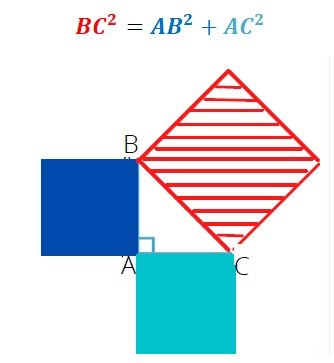
Ceci permet de bien faire la distinction entre l’aire de la surface des carrés formés par les côtés et les longueurs elles-mêmes de ces côtés. L’élève comprend et mémorise ainsi plus facilement.
